Faith and Fate: Transformers as fuzzy pattern matchers
Here at Answer.AI, we are fans of Faith and Fate: Limits of Transformers on Compositionality (aka Dziri et al. 2023, and also presented in this talk). It studies performance on multiplication and a couple other tasks, but in a way that suggests answers to some more fundamental questions: what do transformer-based AI models actually learn? Can they solve complex problems by reasoning systematically through multiple steps?
These are the key questions if we expect these models to do real work by interpreting facts and documents, reasoning about physical systems, business situations, legal problems, medical problems, etc..
Of course the startling fact is that when you read the output of modern frontier models like Claude or GPT-4, they do sound very much like a person who is reasoning, and they solve problems which a person would need to use reasoning to solve. These observations are what amazed everyone who was paying attention in 2023 and what gave rise to the dizzying impression that such models might be, perhaps, on the cusp of human or even superhuman intelligence. But from the beginning it’s also been easy to see that these same models are brilliant at some hard things and stupid at some simple things, so what is actually going on?1
Faith and Fate addresses this empirically. It runs controlled experimental evaluations, proposes its own explanation of what AI models are actually doing – “linearized subgraph matching” – and uses this to explain some failures in informative detail.
While this area of work is known to specialists we feel it deserves a wider audience, so this post will summarize part of the paper to share this point of view. Time to delve! (😛)
Linearized subgraph matching
So what is “linearized subgraph matching”? You will be forgiven for not recognizing this concept, as it has zero hits on Google unrelated to the paper itself. It is their own description of what modern language models are doing, of how they are “thinking”. Here is the gist of it:
- Problem-solving of any task can be represented as a directed graph, which describes the task as a collection of steps, where the steps are solved individually and their results are then put together.
If the overall task’s solution process can be described by a graph, then subtasks within it are subgraphs within that graph. The graph structure describes which steps depend on other steps, and that dependency ordering constrains how the subgraphs may be flattened into a linear sequence.
GPT-like models often “solve” these subgraphs simply by approximate matching. Given a problem which can be described in terms of subgraphs, the models predict by roughly matching it to similar subgraphs in their training data.
The authors tested three tasks, multiplication, the Einstein logic puzzle, and a dynamic programming problem. They are all interesting. To explain this approach more concretely, to see how their experiments support this perspective, and to develop an intuition for what it implies more generally, let us look at the example task of multi-digit multiplication.
What they tested
Multiplication is an apt choice of task, when seen in the context of the optimistic expectation that large models can learn anything with enough data, or that they are solving complex, multistep problems by reasoning in a systematic way. If you believed this, then here’s what you might expect:
- Models should be able to learn multiplication with enough examples (in their training set or in prompts) or with sufficient explanation of the algorithm
- Since multiplication problems are solved by breaking them down into smaller problems, using the well-defined process of the multiplication algorithm, models should be able to solve these problems via step-by-step reasoning using that algorithm.
Did it work out this way? No. But multiplication is so simple that we can nevertheless see where the models fail and what they are doing instead – that is, what they are doing which looks like normal multiplication, when they fail or only partially succeed.
Here’s what the authors did, and what they found. First, to examine the task of multiplying two multi-digit numbers, they defined a large set of multiplication problems. This ranged from 2x2 products (two-digit numbers multiplied by other two-digit numbers) up to 5x5 products.
So they asked models to solve problems like this one:
Question: what’s 35 times 90? Answer: 3150.
Second, they provided the model with examples of how to perform this task by decomposing it into smaller tasks, using the standard multiplication algorithm which children are taught in school. This they call a “scratchpad prompt” but you could also call it chain of thought. By working through the procedure verbally, the model is able to perform subtasks and develop intermediate results on the scratchpad of its own emerging output.
For example, these were the instructions to a model to multiply two numbers (this figure and all others are quoted from the paper):

But how do you say how much one task is more difficult than another? And how do you track where and how a model fails? This is an interesting part. As their third step, the authors described the multiplication algorithm itself as a directed graph of basic operations like addition and multiplication. For example, here is the graph representation of the operations involved in multiplying 7 times 49:
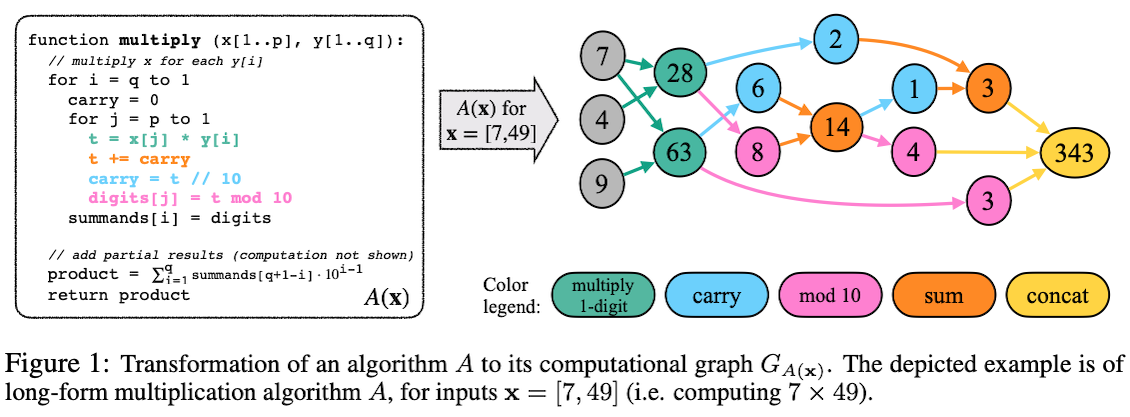
This is a kind of problem decomposition. For instance, if you look within this graph, you can see that the task of multiplying 7 times 49 requires the subtask of multiplying 7 times 4, and that the graph of the larger problem contains the subtask as a subgraph:
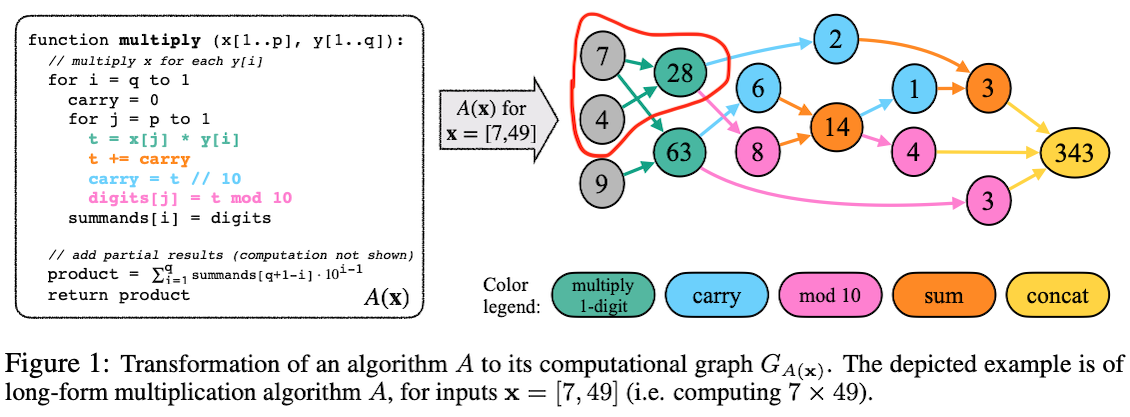
Finally, they evaluated AI models on these tasks, to see where they succeeded and where they failed. They tried finetuning of GPT3 and prompting of GPT4. They also tried zero-shot prompts in addition to the scratchpad-style prompting from above.
What they found
What were the results?
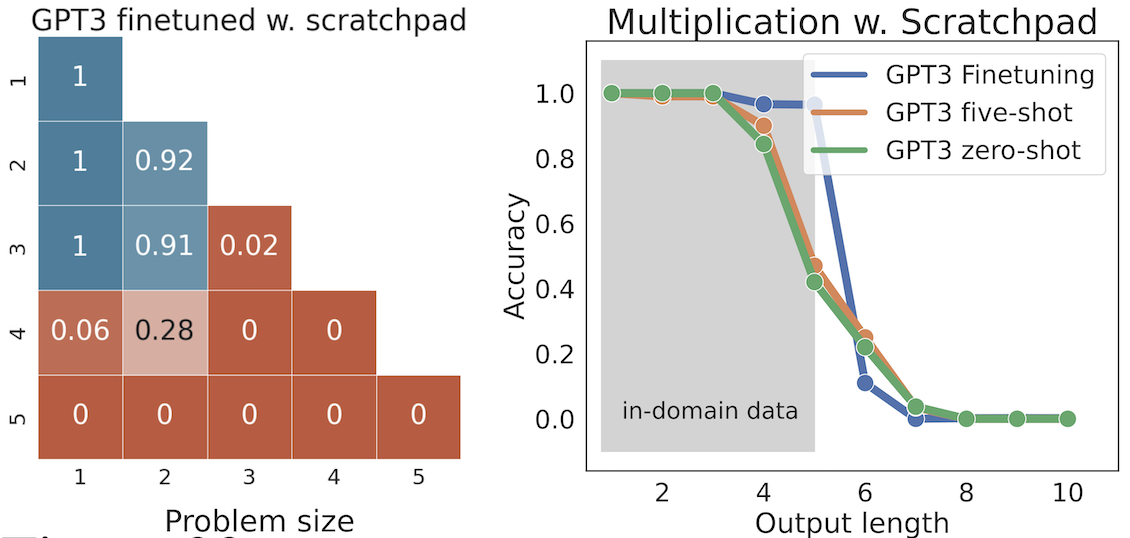
Even with finetuning, the models did not generalize from the small multiplications problems they’d seen in their training set to larger multiplication problems.
In the figure to the left, the column and row labels represent the number of digits in the factors being multiplied. The cells for 1x1, 1x2, 1x3, 2x2, and 2x3, represent predictions on products of 2-digit times 3-digit factors, or smaller. They are blue, to indicate that the model was trained on such products. The scores are pretty good (0.92 to 1) because the models performed well on predicting problems of the same scale as the ones in their training data.
All the other cells, the orange cells, represent products of 3-digit and 3-digit numbers, or products with 4-digit numbers or higher. These cells have much worse scores, because seeing small-digit products did not teach the model how to work out larger-digit products. You can also see the accuracy collapse if you just look at the length, in digits, of the resulting product.
Because every task can be represented by the type of operation graph shown previously, it is also possible to characterize the difficulty of the task in terms of the width and depth of the graph. Roughly, width measures how many intermediate results need to be maintained simultaneously, and depth how long a sequence of steps needs to be composed, in order to reach the result. As with the drop in accuracy from the blue to the orange cells, here also one sees accuracy drop sharply as the task becomes more demanding:
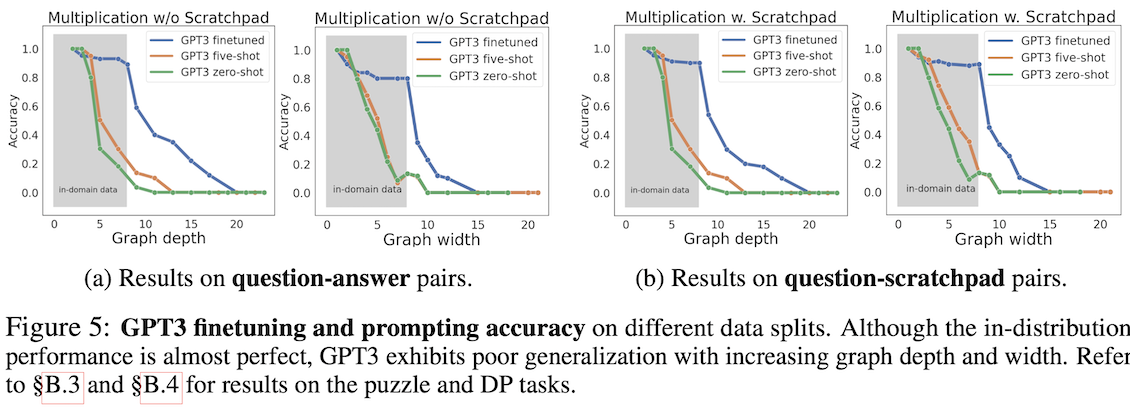
This general result (that GPT models are bad at math) may be old news to you but the next part of the analysis, which describes the pattern of errors, has some less familiar insights.
Errors show what’s really happening
Section 3.2, “Breaking Down Success and Failures of Transformers”, summarizes what the pattern of error seems to suggest.
The first notable observation is that problem-solving success depended on if models had seen relevant subproblems previously. In other words they observed
that models would fail to solve large problems because they solved only some of the larger problem’s subproblems;
that, in particular, they succeeded at solving the subproblems which appeared more frequently or more exactly in the training data, suggesting they were solving them just by recalling them
To follow the previous example, if you ask a model to multiply 7 × 49, and it fails overall, but makes some progress by multiplying 7 × 4, that may be simply because the model has already seen 7 × 4 = 28, and is just remembering that subproblem.
The larger implication here is this: rather than think of models as working through the parts of a problem in a general and systematic way, it is often more accurate to think of them as search engines, recalling examples which roughly match that specific part of a problem before, and then stitching together such approximate recollections.
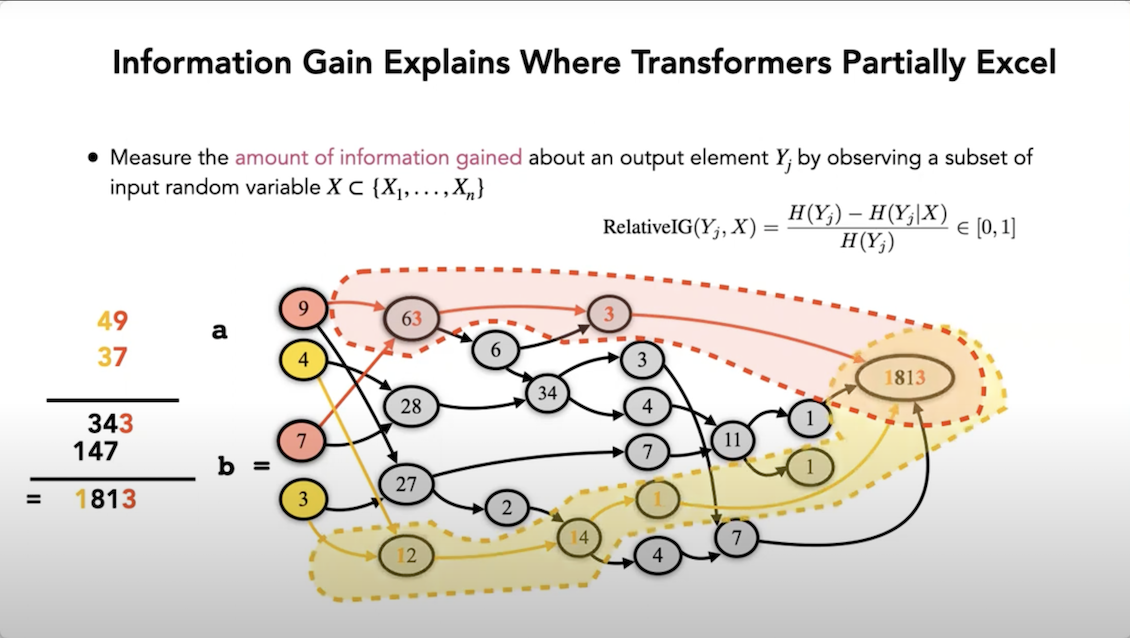
Section 3.2.1 of the paper makes this more precise by providing an information theoretic analysis of this observation, noting that more frequent patterns were predicted more accurately based on “relative information gain”. To put it crudely, you can literally count how often similar subpatterns appeared in the training data, and use that to understand the patterns the models were likely to match.
The second notable observation about the errors is this: yes models solve parts of problems by noticing repeated patterns, but often not the patterns you’re expecting. In particular, it was observed that the decomposition of the problem described by the authors, encoded in the graph representation, and lovingly spoon-fed to the model through the prompt, was often ignored.
The models would achieve partial successes by completing only other subparts of the overall problem. In other words, models solved parts of the problem by decomposing the problem in their own, counter-intuitive, more superficial, but more pragmatic way. Instead of thinking systematically through the multiplication algorithm as given, they’d pick up on more superficial patterns closer to the “surface” of the text.
For instance, in multiplication, the models notice more superficially obvious patterns regarding which digits mostly affect other digits. For instance, “the prediction of the last digit (or two digits) of the output is observed to solely rely on the last digit (or two digits) of each input number. This pattern holds true due to the principles of modulo arithmetic, which ensures the validity of this relationship in all cases”. This is explained clearly in their video (around 23m00s), which shows how the models excelled at certain unexpected solutions
What this means
To summarize, we’re left with the following observations:
- Transformers do not directly and simply follow systematic instructions as systematic instructions.
- They can be prompted to decompose problems into subproblems, and to some extent may do this themselves.
- However, they fundamentally solve many problems by a kind of fuzzy matching.
- Sometimes this is externally indistinguishable from reasoning, sometimes it produces only partial results, and sometimes it goes quite wrong.
I find this to be a helpful set of intuitions!
Right now (July 2024), I expect they are also likely to be obvious intuitions to researchers and practitioners focused closely on this issue, even while they are probably quite unfamiliar to many informed observers.
This is natural because we’re all still figuring this out. Also, it’s a counter-intuitive technology. These models are so deceptively fluent that it takes study to unlearn the first impression they create, increasing the gap between an informed and a naive understanding.
But Faith and Fate, and other papers in its genre, pretty clearly refute the naive idea of what GPT-like models do. These models are not thinking just like we do. They are not even thinking in the way they are describing their thinking. In particular, they do not learn a multistep, algorithmic procedure like multiplication, in the way a person would, the way we mean when we talk about a person “learning multiplication”, the way which results in being able to multiply large numbers as reliably as smaller ones.
The paper shows the same sort of behavior in two other example tasks as well, the Einstein logic puzzle and a dynamic programming problem. And other papers in this genre fit roughly into this pattern as well, including those papers which focus more specifically on reasoning, which is perhaps just an important kind of multistep problem.
What remains unclear
While the paper offers insightful suggestions for thinking about what the models actually are doing, with its idea of subgraph matching, this is more a starting point than a precise or complete picture of the situation.
For instance, subsequent empirical work undermines the generality of this explanation. McLeish et al. (2024) show that you can dramatically improve transformer performance on arithmetic by using a few architectural modifications, such as “abacus embeddings,” which make it easier for a model to track the place value of digits. These modifications allow models to solve multi-digit addition problems which are much larger than the ones presented in their training data, but they do not lead to an equivalent improvement in multiplication. If linear subgraph matching is a general limitation of transformers, then would addition be so amenable to a specific fix? Any why not multiplication?
These sorts of questions point to the specific importance of representation in determining the model’s capability for a specific task, perhaps weakening the argument for a coherent, cross-task capability for reasoning or multistep problem-solving.
And this also points to underlying conceptual ambiguities. For instance, what kind of fuzzy or approximate matching is this subgraph matching, exactly? What does that imply about the textual representation which would make it easier for a model to tackle multistep problems – for instance, chain-of-reasoning problems? This is just the theoretical phrasing of one of the key practical questions of the moment: how should I prepare my training data or my few-shot prompt examples in order to maximize model performance?
And what is a useful way to think about systematic problem-solving? I have liberally used the words “systematic” and “algorithmic” to describe what language models don’t do (just as much of this literature does) but without defining those terms (just as much of the literature doesn’t!). Perhaps a better question is, what’s the practical limit of systems which from the outside look like they’re reasoning, even when we know there is internally no implementation of a search over the space of logical implications?
One final thing I love about this paper: I feel like it has left me with much better questions.
References
Footnotes
Mollick has memorably described this in terms of the “jagged frontier” of AI capabilities – an imagined wall separating what AI can and cannot do. The wall is jagged and invisible, making its contours unpredictable, so near this frontier you can’t easily guess which side any given task will fall on.↩︎